cs231n的第二次作业因为各种课以及考试中断了很久，在一切结束后接上来总是有种力不从心的感觉。assignment 2 涉及到的知识点太多了，神经网络中的各种tricks，sgd加速，batch normalization，drop out等。神经网络以及卷积神经网络各层的前向传播以及后向传播。涉及到传播的可能需要复杂的公式推导以及扎实的python编程基础，所以做起来还是很头疼，但是前面的各种tricks也是让我涨姿势了~ 这里就把最优化的一些知识点小结一下。

梯度下降法

梯度下降法先随机给出参数的一组值，然后更新参数，使每次更新后的结构都能够让损失函数变小，最终达到最小。在梯度下降法中，目标函数其实可以看做是参数的函数，因为给出了样本输入和输出值后，目标函数就只剩下参数部分了，这时可以把参数看做是自变量，则目标函数变成参数的函数。

SGD

批量梯度下降法在更新每一个参数时，都需要所有的训练样本，所以训练过程会随着样本数量的加大而变得异常的缓慢，所以提出了随机梯度下降（SGD）算法。SGD就是每一次迭代计算mini-batch的梯度，然后对参数进行更新。

$$g_t=\nabla_{\theta_{t-1}}{f(\theta_{t-1})}$$ $$\Delta{\theta_t}=-\eta*g_t$$

其中 $\eta$是学习率，$g_t$是梯度

随机梯度下降与传统的梯度下降相比，随机梯度下降法收敛速度速度更快，但是也更容易收敛到局部最优点。除此之外学习率的设置也会极大的影响最终结果。

Momentum

momentum是模拟物理里动量的概念，积累之前的动量来替代真正的梯度。公式如下：

$$m_t=\mu*m_{t-1}+g_t$$ $$\Delta{\theta_t}=-\eta*m_t$$

其中$\mu$是动量因子，作用是通过历史搜索方向的积累，消除相继搜索方向中相反的方向，而一致的方向则相互累加。
与普通的SGD相比，下降初期由于使用上一次参数更新，下降方向一致，乘上较大的$\mu$能够进行很好的加速;而下降中后期时，在局部最小值来回震荡的时候，$gradient\to0$，$\mu$使得更新幅度增大，跳出陷阱。总而言之，momentum项能够在相关方向加速SGD，抑制振荡，从而加快收敛。

Nesterov

将momentum方法的公式展开得：

$$\Delta{\theta_t}=-\eta*\mu*m_{t-1}-\eta*g_t$$

可以看出，$m_{t-1}$并没有直接改变当前梯度$g_t$，所以Nesterov的改进就是让之前的动量直接影响当前的动量。即：

$$g_t=\nabla_{\theta_{t-1}}{f(\theta_{t-1}-\eta*\mu*m_{t-1})}$$ $$m_t=\mu*m_{t-1}+g_t$$ $$\Delta{\theta_t}=-\eta*m_t$$

所以，加上nesterov项后，梯度在大的跳跃后，进行计算对当前梯度进行校正。momentum方法在红色圆圈点通过得到的动量和梯度放下来得到梯度下降的step，而Nesterov则是在预估出actual step之后再对梯度的方向进行计算和校正。（图片引自cs231n Lecture Notes）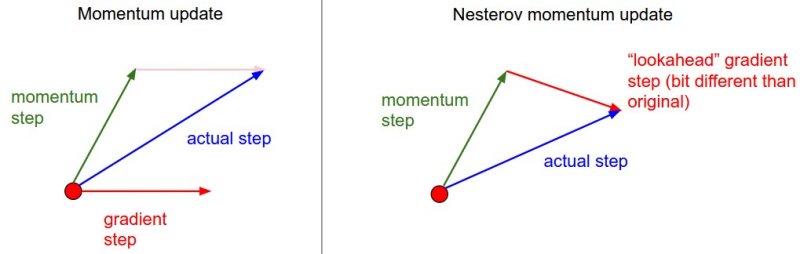

momentum项和nesterov项都是为了使梯度更新更加灵活，对不同情况有针对性。但是这两种方法和SGD一样都需要人工设置学习率，接下来的几种方法可以自适应学习率。

Adagrad

adagrad其实是对学习率进行了一个约束：

$$n_t=n_{t-1}+g_t^2$$ $$\Delta{\theta_t}=-\frac{\eta}{\sqrt{n_t+\epsilon}}*g_t$$

此处，对gt从1到t进行一个递推形成一个约束项regularizer，$-\frac{1}{\sqrt{\sum{r=1}^t(g_r)^2+\epsilon}}$，$\epsilon$用来保证分母非0。

前期当$g_t$较小时，regularizer较大，能放大梯度，而后期$g_t$较大，能约束梯度。Adagrad方法仍需设置一个全局学习率，而$\eta$设置过大也会使regularize过于敏感，对梯度调节太大。

RMSprop

为了解决Adagrad方法后期学习率消失的问题。与Adadelta中计算所有梯度的均方和不同的是，Rprop将之前所有$g_t$的期望和与当前的$g_t$作了一个加权平均：

$$E[g^2]_t = \gamma E[g^2]_{t-1} + （1-\gamma） g^2_t$$ $$\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t}$$

RMSprop的学习率按照梯度的均方和呈指数衰减。Hinton提出$\gamma$设为0.9，$\eta$设为0.001s此算法效果较好。

Adam

Adam(Adaptive Moment Estimation)本质上是带有动量项的RMSprop，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。公式如下：

$$m_t=\mu*m_{t-1}+(1-\mu)*g_t$$ $$n_t=\nu*n_{t-1}+(1-\nu)*g_t^2$$ $$\hat{m_t}=\frac{m_t}{1-\mu^t}$$ $$\hat{n_t}=\frac{n_t}{1-\nu^t}$$ $$\Delta{\theta_t}=-\frac{\hat{m_t}}{\sqrt{\hat{n_t}}+\epsilon}*\eta$$

其中，$m_t$，$n_t$分别是对梯度的一阶矩估计和二阶矩估计，可以看作对期望$E|g_t|$，$E|g_t^2|$的估计；$\hat{m_t}$，$\hat{n_t}$是对$m_t$，$n_t$的校正，这样可以近似为对期望的无偏估计。 可以看出，直接对梯度的矩估计对内存没有额外的要求，而且可以根据梯度进行动态调整，而$-\frac{\hat{m_t}}{\sqrt{\hat{n_t}}+\epsilon}$对学习率形成一个动态约束，而且有明确的范围。

Adam方法结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点，为不同的参数计算不同的自适应学习率。

Batch Normalization

前面提到梯度下降中为了加速收敛，以及避免陷入局部最优一些方法。 在参考文献[3]中提出了Batch Normalization， 它解决了反向传播过程中的梯度问题（梯度消失和爆炸），同时使得不同scale的 权重$w$ 整体更新步调更一致，从而克服深度神经网络难以训练的弊病。

统计机器学习中的一个经典假设是“源空间（source domain）和目标空间（target domain）的数据分布（distribution）是一致的”。因此我们需要对输入数据进行归一化的处理。但是不同的网络层具有不同的特点，如果简单的将每一层都归一化就会失去不同卷积层的区分性。于是[3]中提出了变换重构，引入了参数$\gamma$,$\beta$:

$$y^{(k)} = \gamma^{(k)} + \beta^{(k)}$$

引入这两个参数之后可以使网络学习会服从原始网络的特征分布。（图片引自[3]）

训练过程如：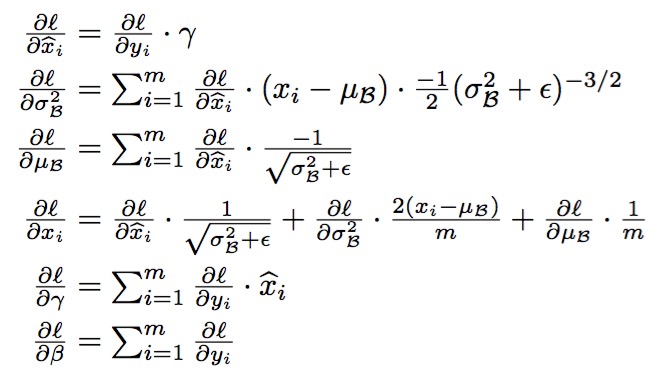

具体说来，在神经网络训练时遇到收敛速度很慢，或梯度爆炸等无法训练的状况时可以尝试BN来解决。另外，在一般使用情况下也可以加入BN来加快训练速度，提高模型精度。

牛顿法与拟牛顿法

除了梯度下降法，牛顿法也是机器学习中用的比较多的一种优化算法。牛顿法的基本思想是利用迭代点处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似，然后把二次模型的极小点作为新的迭代点，并不断重复这一过程，直至求得满足精度的近似极小值。牛顿法的速度相当快，而且能高度逼近最优值。

牛顿法

牛顿法主要有两个应用方向，目标函数最优化求解以及方程的求根，这两个应用方面都主要是针对f(x)为非线性函数的情况。在机器学习最优化的领域中用到的是前一种。牛顿法的核心思想是对函数进行泰勒展开。

对f(x)进行二阶泰勒公式展开：

$$f(x)\approx f(x_k)+f'(x_k)(x-x_k)+\frac{1}{2}f''(x_k){(x-x_k)^2}$$

此时，将非线性优化问题 min f(x) 近似为为二次函数的最优化求解问题：

$$\min f(x_k)+f'(x_k)(x-x_k)+\frac{1}{2}f''(x_k){(x-x_k)^2}$$

对于上式的求解，即二次函数（抛物线函数）求最小值，对函数求导：

$$f'(x_k)+f''(x_k)(x-x_k)=0$$ $$\Rightarrow{x_{k+1}}={x_k}-\frac{1}{f''(x_k)}f'(x_k)$$

从本质上来讲，最优化求解问题的迭代形式都是： ${x_{k+1}}={x_k}-kf’(x_k)$，其中k为系数，$f’(x_k)$为函数的梯度（即函数值上升的方向），那么$-f’(x_k)$为下降的方向，最优化问题的标准形式是：求目标函数最小值，只要每次迭代沿着下降的方向迭代那么将逐渐达到最优，而牛顿将每次迭代的步长定为：$1/f’’({x_k})$。

$$f(x){\approx}f({x_k})+f'({x_k})(x-{x_k})$$

如果这里的x是一个向量， $f’’({x_k})(x-{x_k})$应该写成：${(x-{x_k})^T}f’’(x_k)(x-{x_k})$，$f’’(x-x_k)$为Hessian矩阵。

拟牛顿法

牛顿法是二阶收敛，虽然收敛速度快但是由于计算过程中需要求解目标的二次偏导数，计算复杂度较大。而且有时目标函数的海森矩阵无法保持正定，从而使牛顿法失效。为了克服这两个问题，人们提出了”拟牛顿法”。这个方法的基本思想是：不用二阶偏导数而构造出可以近似海森矩阵（或海森矩阵逆）的正定矩阵，在“拟牛顿”的条件下优化目标函数，不同的构造方法就产生的不同的拟牛顿法。

在介绍几种拟牛顿算法之前，先引出“拟牛顿条件”。设经过$k+1$次迭代后得到$x{k+1}$，此时将目标函数$f(x)$在$x{k+1}$附近作泰勒展开，取二次近似得：

$$f(x)\approx f(x_{k+1})+\bigtriangledown f(x_{k+1})\cdot(x-x_{k+1}) + \frac{1}{2}\cdot(x-x_{k+1})^T \cdot \bigtriangledown^2f(x_{k+1})\cdot (x-x_{k+1})$$

对上式两边同时作用一个梯度算子$\bigtriangledown$,可得：

$$\bigtriangledown f(x) \approx \bigtriangledown f(x_{k+1})+H_{k+1}\cdot(x-x_{k+1})$$

取$x=x_k$并整理，可得:

$$g_{k+1} - g_k \approx H_{k+1} \cdot (x_{k+1} - x_k)$$

令: $s_k = x_{k+1}- x_k, y_k = g_{k+1} - g_k$
则可得:$y_k \approx H_{k+1}\cdot s_k$或者$s_k\approx H_{k+1}^{-1} \cdot y_k$

DFP 算法

DFP是UI早的拟牛顿法，该算法的核心是:通过迭代的方法，对$H_{k+1}^{-1}$（记为$D_{k+1}$）做近似，迭代格式为：

$$D_{k+1} = D_k + \Delta D_k, k=0,1,2,...$$

其中$D_0$通常取为单位矩阵$I$,为了构造一个正定对称的$\Delta D$，将$\Delta D$待定为

$$\Delta D_k=\alpha uu^T+\beta vv^T$$

其中
$\alpha = \frac{1}{s_k^Ty_k}$, $\beta=-\frac{1}{y_k^TD_ky_k}$
我们构造出的校正矩阵

$$\Delta D_k = \frac{s_k s_k^T}{s_k^Ty_k} - \frac{D_ky_ky_k^TD_k}{y_k^TD_ky_k}$$

BFGS 算法

与DFP算法相比，BFGS算法性能更佳，目前它已成为了求解无约束非线性优化问题最常用的方法之一。BFGS算法已有较完善的局部收敛理论。

BFGS算法中核心公式的推导过程与DFP完全类似，只是互换了$s_k$与$y_k$的位置。BFGS算法直接逼近海森矩阵，即$B_k \approx H_k$,设迭代格式为

$$B_{k+1} = B_k + \Delta B_k$$

其中的$B_0$也常取为单位矩阵$I$,将$\Delta B_k$待定为：

$$\Delta B_k = \alpha u u^T + \beta v v^T$$

其中
$\alpha = \frac{1}{y_k^T}$, $\beta = -\frac{1}{s_k^T B_ks_k}$得到了如下校正矩阵

$$\Delta B_k = \frac{y_k y_k^T}{t_k^Ts_k} - \frac{B_ks_ks_k^TB_k}{s_k^TB_ks_k}$$

如果要用$\Delta D_k$来替换$\Delta B_k$，则上式可改为:

$$D_{k+1} = (I - \frac{s_k y^T_k}{y^T_ks_k})B_k^{-1}(I - \frac{y_ks_k^T}{y^T_ks_k}) + \frac{s_k s_k^T}{y_k^T s_k}$$

L-BFGS 算法

在BFGS算法中，需要用到一个$N \times N$的矩阵，当$N$很大时，计算机需要耗费很大资源。L-BFGS就是为了这个解决这个问题。 它对BFGS算法进行了近似，其基本思想是：不再存储完整的矩阵$D_k$，而是计算过程中的最新$m$个向量序列${s_i}$,${y_i}$,需要矩阵$D_k$时，利用向量序列{s_i}与{y_i}计算来代替。

具体来说,为了实现迭代式

$$D_{k+1} = (I - \frac{s_k y^T_k}{y^T_ks_k})B_k^{-1}(I - \frac{y_ks_k^T}{y^T_ks_k}) + \frac{s_k s_k^T}{y_k^T s_k}$$

记$\rho_k = \frac{1}{y_k^T}$, $V_k = I- \rho_ky_ks^T_k $，L-BFGS算法流程可描述如下[7]：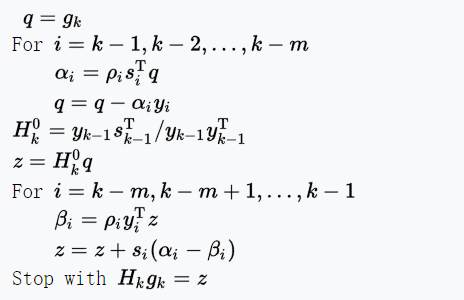

参考文献

1. 深度学习最全优化方法总结比较（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）
2. An overview of gradient descent optimization algorithms
3. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
4. 深度学习中 Batch Normalization为什么效果好？魏秀参的回答
5. Batch Normalization 学习笔记 - hjimce
6. 牛顿法与拟牛顿法学习笔记（一）牛顿法
7. Limited-memory BFGS - Wikipedia