Spectral Graph Algorithm 学习小结

2017-08-04

上周被老师派去了上海交大进行了为期一周的summer school，学习的主题是“算法谱图论”。由于去之前也没有提前准备图论的知识，上课的过程显得有些被动。万幸是研一还是认真上过矩阵论，也接触过了一些算法，所以勉强能够跟上整个课程的节奏：基本概念还是知道了个大概，但是证明的细节我也确实没有去深究了。这里把我一周学习的内容做一个小结。

算法谱图论是什么

wiki给出的解释是：“In mathematics, spectral graph theory is the study of the properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated with the graph, such as its adjacency matrix or Laplacian matrix. ” 孙老师给我们讲的是，算法谱图论旨在用代数与几何的方法来表示“图”这个数据结构并探究图的内在特征。具体来说算法谱图论需要一些关于矩阵的基础，包括特征值，特征向量，矩阵多项式等；除此之外对解析几何也有一定要求，解析几何部分的内容可以将算法直观化。

算法谱图论的基本内容

从7月25日到7月29日，我们每天上午下午各上两个小时课,一共就是上了十节课，学习的内容的涉及面也比较广。总结下可能主要涉及到相关概念，谱性质与谱聚类和谱稀疏这三个大块来讲的。

谱性质

cheeger常数与cheeger不等式

一个d-regular图中某个节点集$S \subseteq V$,令$h_G(S)= \frac{|\partial S|}{|S|}$,其中$\partial S= { (x,y) \in E(G): x \in S, y \in V(G)\S } $。cheeger常数定义为$h(G) = \min_S h_G(S)$。从概率的角度看，这正是随机选取一个节点集$S$中顶点的边，那么边的‘扩展’到节点集$S$外的概率。使用拉普拉斯矩阵的第二小特征值$\lambda_2$可以将图的cheeger常数进行限定，具体说来可表示为cheeger不等式:

$\frac{\lambda_2}{2} \leqslant h(G) \leqslant \sqrt{2\lambda_2}$

Cheeger常数为正当且仅当G是完全图(connected graph),cheeger常数是值很小的正数表明该图存在一个”瓶颈”。考虑一个环形网络入图2所示,这个环的节点顺时针编号为1,2,3…顶点集和边的集合可以表示为：

$V(G_N) = \left \{1,2,3...,N-1, N \right \}$ $E(G_N) = \left \{ (1,2),(2,3),...,(N-1,N),(N,1)\right \}$

令$S$为这个连环链路中的$ \left \lfloor \frac{N}{2} \right \rfloor$个点，即：

$S = \left \{ 1,2,...,\left \lfloor \frac{N}{2} \right \rfloor \right \}$ $\partial S = \left \{ (\left \lfloor \frac{N}{2} \right \rfloor,\left \lfloor \frac{N}{2} \right \rfloor+1),(N,1)\right \}$

当N趋近于$\infty$时，$\frac{|\partial S|}{|S|}$趋近于0。事实上，小的Cheeger常数就表示整个图会因为某一个点而影响整个性能。这个环形网络如果有一个节点崩掉了，那整个网络都不能互相通信了，这是我们不愿意发生的。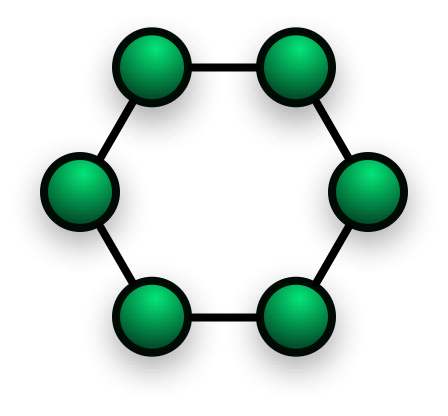
图3.2 环形网络

谱扩展

扩展图(expand graph)是一系列有高可扩展性的稀疏图。由于稀疏性意味着更少的建造成本，高的可扩展性意味着高的连通性，所以扩展图的技术最开始被应用到低成本通信网络的构造。
构造扩展图的基本思想就是利用两个图之间顶点，边和度的关系来让新的图尽可能拥有原始图的特征。孙老师上课的时候提到了两种构造图的方法：置换积（Replacement Product）和之子积（Zig-Zag Product）.对于有$N$个定点，$M$条边，$D$度的大图$G$和$n$个定点，$m$条边，$d$度的小图$H$，用置换积构造的图会有$N \times n$个定点，$ M \times m $条边，$D$度；而用之子积构造的图会有$N \times D$个定点，$d^2$度，$M-1$条边。总体来说，置换积的度仅取决于小图的度，它可以用来在不丢失图的连通性的条件下减小图的度，而之子积继承了大图的大小，继承了小图的度，而扩展性则综合了大图和小图的特性，所以之子积可以用来建立具有有界度和良好扩张性质的大图。

谱聚类和谱稀疏

谱聚类和谱稀疏是孙老师最后讲的两个部分，这两块在很多方面都有应用，而且也是现在的研究热点。

一个网络中聚类之间的连通率（conductance）往往可以评判网络之间的通信性能。（原句是Clusters of low conductance in networks appearing in practice usually capture the notation of community），寻找聚类的算法也经常被应用到通信检测和网络分析等方面。K聚类问题就是把一个图分为K部分，每一部分的cheeger 常数（conductance）都很小。谱聚类算法利用了图的割(cut)与图正则化拉普拉斯矩阵的特征向量的关系，即结构定理(The Structure Theorem )。

稀疏图(sparse graph)表示边的数量和点的数量几乎成正比的图。由于大部分算法在稀疏图上运行的时间更少，同时稀疏图也更节省存储空间，所以将一个图G转换为特征相似的稀疏图H是有必要的。 Spielman-Srivastava算法可以通过特定概率来采样原图的边，从而得到稀疏图，但这种方式计算复杂度相对较大。除此之外，孙老师所在的组最近也提出了线性时间的谱稀疏算法。

算法谱图论的应用

总的来说，算法谱图论其实就是就是研究图上的一些代数或是几何特性，所以只要某个object可以用graph来表示出来，那么就可以用算法谱图论的一些算法来解决问题。具体来说可能有下面几个方面：

图像分割(Image segementation)，用cheeger常数可以算出图的最小割，从而得到相应的分割线，但是这个分割可能并不理想。
PageRank 通过将网络中网页之前互联的关系表示成邻接矩阵，可以用矩阵的特征来获得链接的排序。
网络通信 前面提到的扩展图与图的分割，涉及到建造优性能网络的问题。
社交网络 通过将人与人之间的互联关系建模，对用户进行基于某种特性的分类。(graph clusting)
数据集合并 用谱扩展(Construction of Expander Graphs)的方法可以在较短时间内将来源不同的数据集合成新的数据集。

学习体会

这次学习的最大体会就是，千万不要高估了自己，有好多比你聪明得多的人比你还要努力。在上交的室友是个大四的妹子，可是去年就已经发了一篇A类的论文还是best paper award，才大四已经在准备托福要研究生毕业出国了。还有上课时坐在前面的一群复旦的妹子，长得好看不说，一下课就在讨论上课的内容，关键是讨论的东西我还不怎么能听得懂（T.T），有一种我的大学四年是不是白学了的感觉~ 诚然，数学功底和英语功底在做研究这个方面至关重要，但是最重要的还是与优秀的人交流。如果只是呆在华科，与实验室的学长比，或是跟选同一门课的同学比（没错我说的就是软件无线电课），可能我是会有一些优越感。呆在一个自我感觉良好的地方未必是好事，久而久之毕竟会消磨你的斗志和上进心。在下半年再给自己立一个flag，在自己的研究方向阅读大量文献并思考提出问题，与文章作者进行email交流并有所收获。嗯，愿自己变得更优秀。